Sierpinski 镂垫程序

Posted on | In | 1.3k | 6 分钟

用C++实现三个 Sierpinski 镂垫程序

Sierpinski镂垫是一个非常有趣的图案，有着悠久的历史， 在分形几何中等领域里引起了人们极大地兴趣， 是用递归和随机方式定义的几何形状。

生成算法如下：

  1. 在三角形内部随机选取一个点作为初始点；
  2. 在三角形的3个顶点中随机选取一个，求出该顶点与初始点连线的中点，画出该中点；
  3. 将第二步中的中点作为初始点，循环第二步；

1 二维Sierpinski镂垫

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/*使用随机选择的顶点和中点绘制二维Sierpinski镂垫*/
#include <windows.h>
#include <GL/glut.h>

void myinit()
{
  glClearColor(1.0,1.0,1.0,1.0);/*白色背景*/
  glColor3f(1.0,0.0,0.0);/*红色*/

  glMatrixMode(GL_PROJECTION);
  glLoadIdentity();
  gluOrtho2D(0.0,50.0,0.0,50.0);/*50×50相机坐标窗口与原点左下角*/
  glMatrixMode(GL_MODELVIEW);

}

void display()
{
  GLfloat vertices[3][2]={{0.0,0.0},{25.0,50.0},{50.0,0.0}};

  int j,k;
  int rand();/*产生随机数*/
  GLfloat p[2]={7.5,5.0};/*在三角形内任意初始点*/
  glClear(GL_COLOR_BUFFER_BIT);/*清理窗口*/

  glBegin(GL_POINTS);/*产生5000个新点*/

  for(k=0;k<5000;k++)
  {
    j=rand()%3;/*随机选择一个顶点*/
    /*计算点位于选定顶点和旧点之间*/
    p[0]=(p[0]+vertices[j][0])/2.0;
    p[1]=(p[1]+vertices[j][1])/2.0;
    /*画新点*/
    glVertex2fv(p);
  }
  glEnd();
  glFlush();/*清除缓冲帧*/
}

int main(int argc,char *argv[])
{
  glutInit(&argc,argv);/*标准的GLUT初始化*/
  glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);/*默认设置*/
  glutInitWindowSize(500,500);/*500×500像素窗口*/
  glutInitWindowPosition(0,0);/*将窗口放在左下角*/
  glutCreateWindow("Sierpinski Gasket");/*窗口名*/
  glutDisplayFunc(display);/*窗口打开时调用的显示回调*/
  myinit();/*设置属性*/
  glutMainLoop();/*进入事件循环*/
}

结果

2 生成 Sierpinski 镂垫的递归程序

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/* 通过细分三角形的方法生成Sierpinski镂垫 */
/* 通过命令行输入递归的次数 */
#include <GL/glut.h>
#include<stdlib.h>
/* 初始的三角形 */
GLfloat v[3][2]={{-1.0, -0.58}, {1.0, -0.58}, {0.0, 1.15}};
int n;
void triangle( GLfloat *a, GLfloat *b, GLfloat *c)
/* 定义某个三角形 */
{
 glVertex2fv(a);
 glVertex2fv(b);
 glVertex2fv(c);
}
void divide_triangle(GLfloat *a, GLfloat *b, GLfloat *c, int m)
{
/* 基于某个顶点的数量对三角形进行细分处理 */
 GLfloat v0[2], v1[2], v2[2];
 int j;
 if(m>0)
 {
 for(j=0; j<2; j++) v0[j]=(a[j]+b[j])/2;
 for(j=0; j<2; j++) v1[j]=(a[j]+c[j])/2;
 for(j=0; j<2; j++) v2[j]=(b[j]+c[j])/2;
 divide_triangle(a, v0, v1, m-1);
 divide_triangle(c, v1, v2, m-1);
 divide_triangle(b, v2, v0, m-1);
 }
 else triangle(a,b,c); /* 递归结束时绘制三角形 */
}
void display(void)
{
     glClear(GL_COLOR_BUFFER_BIT);
         glBegin(GL_TRIANGLES);
         divide_triangle(v[0], v[1], v[2], n);
         glEnd();
     glFlush();
}
void myinit()
{
     glMatrixMode(GL_PROJECTION);
     glLoadIdentity();
     gluOrtho2D(-2.0, 2.0, -2.0, 2.0);
     glMatrixMode(GL_MODELVIEW);
     glClearColor(1.0, 1.0, 1.0, 1.0);
     glColor3f(0.0,0.0,0.0);
}
main(int argc, char **argv)
{
     n=3;    /* 或者在此输入三角形细分的步数 */
     glutInit(&argc, argv);
     glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
     glutInitWindowSize(500, 500);
     glutCreateWindow("Sierpinski Gasket");
     glutDisplayFunc(display);
         myinit();
     glutMainLoop();
}

结果

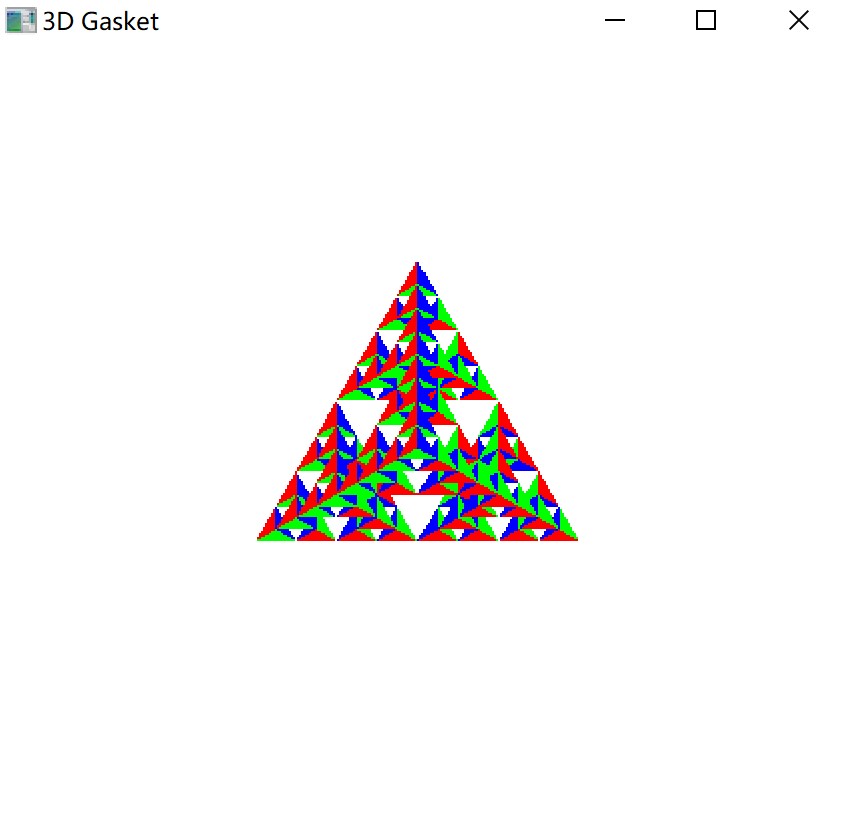
3 三维 Sierpinski 镂垫的递归程序

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/* 通过递归细分四面体方法生成Sierpinski镂垫 */
/* 通过命令行递归的次数 */
#include <stdlib.h>
#include <GL/glut.h>
/* 初始的四面体 */
GLfloat v[4][3]={{0.0, 0.0, 1.0},{0.0, 0.942809, -0.33333},
  {-0.816497, -0.471405, -0.333333},{0.816497, -0.471405, -0.333333}};
GLfloat colors[4][3]={{1.0,0.0,0.0},{0.0,1.0,0.0},
{0.0,0.0,1.0},{0.0,0.0,0.0}};
int n;
void triangle( GLfloat *va, GLfloat *vb, GLfloat *vc)
{
 glVertex3fv(va);
 glVertex3fv(vb);
 glVertex3fv(vc);
}
void tetra(GLfloat *a, GLfloat *b, GLfloat *c, GLfloat *d)
{
 glColor3fv(colors[0]);
 triangle(a,b,c);
 glColor3fv(colors[1]);
 triangle(a,c,d);
 glColor3fv(colors[2]);
 triangle(a,d,b);
 glColor3fv(colors[3]);
 triangle(b,d,c);
}
void divide_tetra(GLfloat *a, GLfloat *b, GLfloat *c, GLfloat *d, int m)
{
 GLfloat mid[6][3];
 int j;
 if(m>0)
 {
   /* 计算六个中点 */
 for(j=0; j<3; j++) mid[0][j]=(a[j]+b[j])/2;
 for(j=0; j<3; j++) mid[1][j]=(a[j]+c[j])/2;
 for(j=0; j<3; j++) mid[2][j]=(a[j]+d[j])/2;
 for(j=0; j<3; j++) mid[3][j]=(b[j]+c[j])/2;
 for(j=0; j<3; j++) mid[4][j]=(c[j]+d[j])/2;
 for(j=0; j<3; j++) mid[5][j]=(b[j]+d[j])/2;
   /* 通过细分生成四个四面体 */
 divide_tetra(a,mid[0],mid[1],mid[2], m-1);
 divide_tetra(mid[0],b,mid[3],mid[5], m-1);
 divide_tetra(mid[1],mid[3],c,mid[4], m-1);
 divide_tetra(mid[2],mid[4],d,mid[5], m-1);
 }
 else   tetra(a,b,c,d); /* 递归结束时绘制四面体 */
}
void display(void)
{
 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
 glBegin(GL_TRIANGLES);
     divide_tetra(v[0],v[1],v[2],v[3],n);
     glEnd();
     glFlush();
}
void myReshape(int w, int h)
{
     glViewport(0, 0, w, h);
     glMatrixMode(GL_PROJECTION);
     glLoadIdentity();
     if (w <= h)
     glOrtho(-2.0, 2.0, -2.0 * (GLfloat) h / (GLfloat) w,
 2.0 * (GLfloat) h / (GLfloat) w, -10.0, 10.0);
 else
     glOrtho(-2.0 * (GLfloat) w / (GLfloat) h,
 2.0 * (GLfloat) w / (GLfloat) h, -2.0, 2.0, -10.0, 10.0);
 glMatrixMode(GL_MODELVIEW);
 glutPostRedisplay();
}
main(int argc, char **argv)
{
 n=atoi(argv[1]);  /* 或者在此处输入四面体细分的步数 */
 glutInit(&argc, argv);
 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
 glutInitWindowSize(500, 500);
 glutCreateWindow("3D Gasket");
 glutReshapeFunc(myReshape);
 glutDisplayFunc(display);
 glEnable(GL_DEPTH_TEST);
 glClearColor (1.0, 1.0, 1.0, 1.0);
 glutMainLoop();
}

结果

-------------------本文结束 感谢您的阅读-------------------
0%