Hill 密码加密解密详解：古典密码与矩阵乘法(C++实现)

Hill密码是多字母代换古典密码，利用矩阵乘法实现加密解密，本文用C++实现Hill密码的加解密流程并解析其数学原理。

希尔密码加密解密原理

  希尔密码是运用基本矩阵论原理的替换密码。每个字母当作26进制数字：A=0，B=1…一串字母当成n维向量，跟一个$n×n$的矩阵相乘，再将得出的结果MOD 26。注意用作加密的矩阵（即密钥）必须是可逆的，否则就不可能译码。只有矩阵的行列式和26互质，才是可逆的。

1 加密的矩阵为随机矩阵

代码

/*hillcrypto.cpp*/
/*理解算法最重要，最好自己动手实现试试看，可以使用MFC写一个简单的交互界面*/

#include <iostream>
#include <string>
#include <memory.h>
#include <cstdlib>
#include <ctime>
#include <cstdio>
#include <cmath>
using namespace std;

/*定义一些常变量*/
const int M = 26;   //定义集合{a,b,...,z}的26个英文字母

//行和列均为5
const int ROW = 5;
const int COL = 5;

//定义5*5的加密矩阵
int K[ROW][COL];

//定义5*5的解密矩阵
int D[ROW][COL];

int P[ROW];  //明文单元
int C[ROW];  //密文单元
int F[ROW];  //密文解密后的单元

/*三元组gcd(a,b) = ax + by = d */
struct GCD
{
    int x;
    int y;
    int d;
};

class Hill_Cipher
{
public:
    //产生随机矩阵
    void random_Matrix();
    //求矩阵的行列式
    int Det(int matrix[ROW][ROW],int row);

    //求两个数的最大公约数
    int gcd(int a,int b);

    /*
     *判断矩阵K是否在模26的情况下可逆
     *因为矩阵在模26的情形下存在可逆矩阵的充分必要条件是
     *gcd(det K,26) = 1
     */
    bool Inverse(int matrix[ROW][ROW]);

    //矩阵相乘
    void multiphy(int matrix[ROW][ROW],int p[ROW],int row);

    //求出伴随矩阵
    void adjoint_matrix(int matrix[ROW][ROW],int row);

    //将明文加密为密文
    string encryption(string plaintext);

    //将密文解密为明文(为了辨识清楚,我们统一以小写字母作为明文,大写字母作为密文)
    string deciphering(string ciphertext);

    //欧几里得算法求模的逆
    GCD extended_Euclid(int a,int b);

    //模逆运算
    int inverse(int a,int m);

    //由于C++不存在负数取模的内置函数,现在自己设定一个
    //定义一个模M的值
    int Mod(int a);
};

void Hill_Cipher::random_Matrix()
{
    int i,j;
    for(i = 0;i < ROW;i++)
    {
        for(j = 0;j < COL;j++)
        {
            K[i][j] = rand() % 26;  //产生一个5*5模26的矩阵
        }
    }

}

//求矩阵的行列式
int Hill_Cipher::Det(int matrix[ROW][ROW],int row)
{
    int i,j;
    int cofa[ROW][ROW];            //用于存放余子阵
    int l;   //l为所递归的余子阵的行
    int p = 0,q = 0;
    int sum=0;

    //由于行和列相同(方阵),所以行列式的值一定存在,故不需要判断是否为方阵

    //递归基
    if(row == 1)
        return matrix[0][0];
   for(i = 0;i < row; i++)
   {
     for(l = 0;l < row - 1;l++)
     {
       if(l < i)
           p=0;
       else
           p=1;
       for(j = 0;j< row - 1;j++)
       {
         cofa[l][j] = matrix[l + p][j + 1];
       }
     }
     //相当于(-1)^i
     if(i % 2 == 0)
         q=1;
     else
         q=(-1);
     sum = sum + matrix[i][0] * q * Det(cofa,row - 1);
   }
   return sum;
}

//求两个数的最大公约数
int Hill_Cipher::gcd(int a,int b)
{
    int temp;
    //交换两个数的大小,使得a为较大数
    if(a < b)
    {
        temp = a;
        a = b;
        b = temp;
    }
    while(a % b)
    {
        temp = b;
        b = a % b;
        a = temp;
    }
    return b;
}

/*
 *判断矩阵K是否在模26的情况下可逆
 *因为矩阵在模26的情形下存在可逆矩阵的充分必要条件是
 *gcd(det K,26) = 1
 */
bool Hill_Cipher::Inverse(int matrix[ROW][ROW])
{
    if(gcd(Det(matrix,ROW),M) == 1)
        return true;
    else
        return false;
}

void Hill_Cipher::multiphy(int matrix[ROW][ROW],int p[ROW],int row)
{
    int i,j;
    //先将密文单元清零
    memset(C,0,sizeof(C));
    for(i = 0;i < ROW;i++)
    {
        for(j = 0;j < ROW;j++)
        {
            C[i] += P[j] * K[j][i];
        }
    }
}

//将明文加密为密文
string Hill_Cipher::encryption(string plaintext)
{
    int i;
    string ciphertext;
    //将字符串转化为明文数组
    for(i = 0;i < ROW;i++)
    {
        P[i] = plaintext[i] - 'a';
    }
    multiphy(K,P,ROW);
    //将密文数组转化为密文
    for(i = 0;i < ROW;i++)
        //这里先将其模26,再翻译为对应的字母
    {
        C[i] =Mod(C[i]);
        ciphertext += C[i] + 'A';
    }
    return ciphertext;
}

//求出伴随矩阵
void Hill_Cipher::adjoint_matrix(int matrix[ROW][ROW],int row)
{
    int i,j,k,l;
    int p,q;
    p = q = 0;
    int temp[ROW][ROW];
    for(i = 0;i < ROW;i++)
    {
        for(j = 0;j < ROW;j++)
        {
            for(k = 0;k < ROW - 1;k++)
            {
                if(k < i)
                    p = 0;
                else
                    p = 1;
                for(l = 0;l < ROW - 1;l++)
                {
                    if(l < j)
                        q = 0;
                    else
                        q = 1;
                    temp[k][l] = matrix[k+p][l+q];
                }
            }
            D[j][i] = (int)pow(-1,(double)i+j)*Det(temp,ROW-1);
            D[j][i] = Mod(D[j][i]);
        }
    }
}

//将密文解密为明文(为了辨识清楚,我们统一以小写字母作为明文,大写字母作为密文)
string Hill_Cipher::deciphering(string ciphertext)
{
    //求出矩阵的逆
    string text;
    int determinant = Det(K,ROW);
    int inver = inverse(determinant,26);
    adjoint_matrix(K,ROW);   //伴随矩阵
    cout << "行列式的值: " << determinant << endl;
    int i,j;
    memset(F,0,sizeof(F));
    for(i = 0;i < ROW;i++)
    {
        for(j = 0;j < ROW;j++)
        {
            F[i] += C[j] * D[j][i];
        }
        F[i] *= inver;
        F[i] = Mod(F[i]);   //算到的结果要模去26
    }
    for(i = 0;i < ROW;i++)
        text += F[i] + 'a';
    return text;
}

GCD Hill_Cipher::extended_Euclid(int a,int b)
{
    GCD aa,bb;
    if(b == 0)
    {
        aa.x = 1;
        aa.y = 0;
        aa.d = a;
        return aa;
    }
    else
    {
        bb = extended_Euclid(b,a%b);
        aa.x = bb.y;
        aa.y = bb.x - (a / b) * bb.y;
        aa.d = bb.d;
    }
    return aa;
}

int Hill_Cipher::inverse(int a,int m)
{
    GCD aa;
    aa = extended_Euclid(a,m);
    return aa.x;
}

int Hill_Cipher::Mod(int a)
{
    return a >= 0 ? a % M : (M + a % M);
}

int main()
{
    int i,j;
    Hill_Cipher hh;
    cout << "使用希尔密码进行消息的加解密:" << endl;

    //srand()函数产生一个以当前时间开始的随机种子.以保证每次产生的随机数矩阵都不相同
    srand((unsigned)time(0));
    hh.random_Matrix();
    while(!hh.Inverse(K))
    {
        hh.random_Matrix();
    }
    cout << "随机产生5*5的矩阵:" << endl;
    for(i = 0;i < ROW;i++)
    {
        for(j = 0;j < COL;j++)
        {
            printf("%2d  ",K[i][j]);
        }
        cout << endl;
    }
    cout << "该矩阵模26可逆,因此可以作为密钥." << endl;
    cout << endl;

    //利用所选密钥，对给定的5元明文信息进行加解密
    string plaintext,ciphertext;
    cout << "请输入5元明文信息:" << endl;
    cin >> plaintext;
    ciphertext = hh.encryption(plaintext);
    cout << endl;
    cout << "该明文通过希尔密码法加密过后,输出的密文消息为:" << endl;
    cout << ciphertext << endl;
    cout << endl;

    cout << "***输入0:退出          ***" << endl;
    cout << "***输入1:查看明文空间对***" << endl;
    cout << "***输入2:查看密文空间对***" << endl;
    cout << "***输入3:查看密钥      ***" << endl;
    cout << "***输入4:将消息解密    ***" << endl;
    cout << "***输入5:查看菜单      ***" << endl;

    char c;
    while(cin >> c)
    {
        if(c == '0')
        {
            cout << endl;
            cout << "退出" << endl;
            break;
        }
        else if(c == '1')
        {
            cout << "明文空间:" << endl;
            for(i = 0;i < ROW;i++)
                cout << P[i] << "  ";
            cout << endl;
            cout << endl;
        }
        else if(c == '2')
        {
            cout << "密文空间:" << endl;
            for(i = 0;i < ROW;i++)
                cout << C[i] << "  ";
            cout << endl;
            cout << endl;
        }
        else if(c == '3')
        {
            cout << "密钥:" << endl;
            for(i = 0;i < ROW;i++)
            {
                for(j = 0;j < ROW;j++)
                {
                    printf("%2d  ",K[i][j]);
                }
                cout << endl;
            }
            cout << endl;
        }
        else if(c == '4')
        {
            hh.adjoint_matrix(K,ROW);
            string ss;
            ss = hh.deciphering(ciphertext);
            cout << "该密文解密过后,显示的原来的明文消息:" << endl;
            cout << ss << endl;
            cout << endl;
        }
        else
        {
            cout << "***输入0:退出          ***" << endl;
            cout << "***输入1:查看明文空间对***" << endl;
            cout << "***输入2:查看密文空间对***" << endl;
            cout << "***输入3:查看密钥      ***" << endl;
            cout << "***输入4:将消息解密    ***" << endl;
            cout << "***输入5:查看菜单      ***" << endl;
        }
    }
    return 0;
}

结果

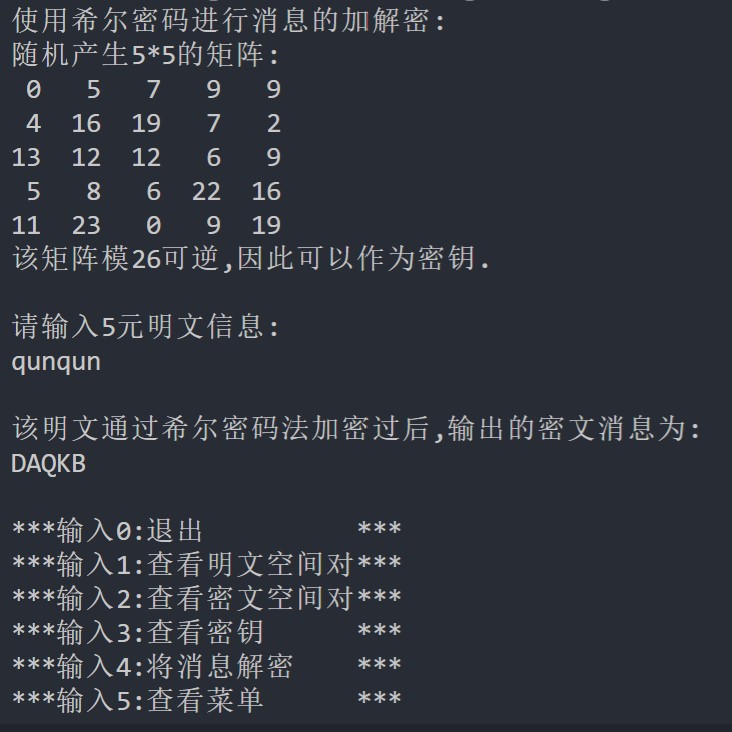
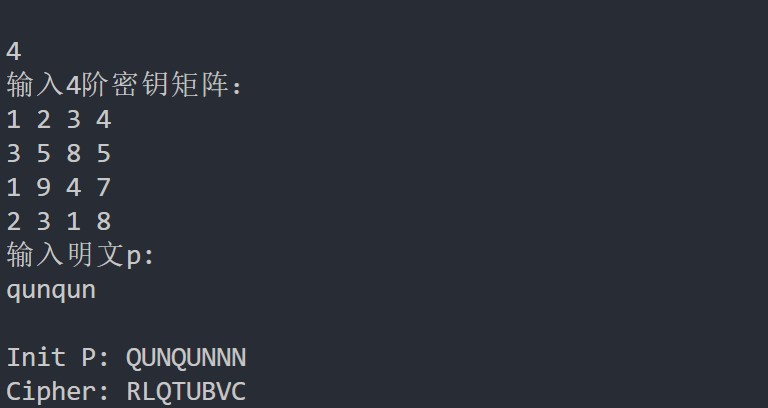
2 加密的矩阵为密钥矩阵

代码

/*hill.cpp*/
#include <iostream>
#include <cstring>
#include <cstdlib>
#define N 100
using namespace std;

//按第一列展开，递归计算行列式值
int caluDet(int n, int **a)
{
    int i, r, c, p, q;
    int sum=0;
    if(n==1)
        return a[0][0];
    int **det = (int**)malloc((n-1)*sizeof(int*));
    for(i=0; i<(n-1); i++)
        det[i] = (int*)malloc((n-1)*sizeof(int));
    for(i=0; i<n; i++) {
        for(r=0; r<n-1; r++) {         //子矩阵 (n-1) 行
            if(r<i) p = 0;              //当前行 a[r] 赋值给子矩阵
            else    p = 1;             //下一行 a[r+1] 赋值给子矩阵
            for(c=0; c<n-1; c++)        //子矩阵 (n-1) 列
                det[r][c] = a[r+p][c+1];
        }
        if(i%2==0) q = 1;               //由于是对第一列展开，即 [i][0]
        else q = -1;
        sum = sum + a[i][0] * q*caluDet(n-1,det);
    }
    for(i=0; i<(n-1); i++)
        free(det[i]);
    free(det);
    return sum;
}

//初始化明文
void initPlain(char p[], int n)
{
    int i, len, t;
    cout << "输入明文p: \n";
    getchar(); gets(p);
    for(i=0; i<strlen(p); i++) {
        if (p[i] ==' ')             //跳过空格
            strcpy(p+i,p+i+1);
        if (p[i]>='a' && p[i]<='z')  //小写转大写
            p[i] -= 32;
    }
    len = strlen(p);
    t = len%n>0 ? n-len%n : len%n;
    while(t--)     //若最后一个明文对字母不足，则添加与最后一个明文相同的字母
        p[strlen(p)] = p[len-1];
    p[strlen(p)] = '\0';
    cout <<"\nInit P: " << p << endl;
}

//输入密钥矩阵
void keyMatrix(int **det, int len)
{
    int i, j;
    for(i=0; i<len; i++)
        for(j=0; j<len; j++)
            cin >> det[i][j];
}

//分组、矩阵乘法
void matricMultiply(char p[], char c[], int **key, int n)
{
    int i,j,k;
    int len = strlen(p);
    for(i=0; i<strlen(p)/n; i++){       //明文每 n 个作为一行
        for(j=0; j<n; j++){             //明文的列、密钥矩阵的列
            for(k=0; k<n; k++){         //密钥矩阵的行
                c[n*i+j] += ((p[n*i+k]-'A') * key[k][j]) % 26;
            }
            c[n*i+j] = c[n*i+j] % 26 + 'A';
            //cout << (int)c[n*i+j] << " ";
        }
    }
    cout << "Cipher: " << c << endl;
}

int main()
{
    int i, j, n, len;
    char p[N]={0}, c[N]={0};
    cout << "输入密钥的阶：\n";
    cin >> n;
    //为密钥矩阵申请内存空间
    int **key = (int**)malloc(n*sizeof(int*));
    for(i=0; i<n; i++)
        key[i] = (int*)malloc(n*sizeof(int));
    //获取密钥矩阵并验证是否可逆
    cout << "输入" <<n<<"阶密钥矩阵：\n";
    keyMatrix(key,n);
    while(!caluDet(n, key)) {
        cout << "密钥不存在逆矩阵! 请重新输入：\n";
        keyMatrix(key,n);
    }
    //初始化明文
    initPlain(p, n);
    len = strlen(p);
    //各组明文乘密钥矩阵加密
    matricMultiply (p, c, key, n);
    //释放密钥矩阵的内存空间
    for(i=0; i<n; i++)
        free(key[i]);
    free(key);
    return 0;
}

结果