Liang-Barsky裁剪算法

Liang-Barsky算法的原理与代码

Liang-Barsky裁剪算法

原理

用参数方程表示一条直线，用方程表示直线$P_{1}P_{2}$，其中$t$就是直线的斜率，$\mathrm{t} \in[0,1]:$

$$ \begin{equation}
\left\{
\begin{aligned}
x(t)=x_{1}+\left(x_{2}-x_{1}\right) t&=x_{1}+t \Delta x \qquad 0<t<1 \\
y(t)=y_{1}+\left(y_{2}-y_{1}\right) t&=y_{1}+t \Delta y \qquad 0<t<1
\end{aligned}
\right.
\end{equation} $$

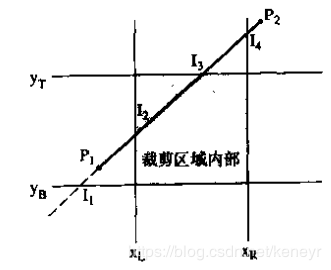裁剪区域内部可以表达为两个不等式：

$$\begin{aligned}
&x_{L}<x<x_{R}\
&y_{B}<y<y_{T}
\end{aligned}$$
把直线方程代入得到不等式：
$$ \begin{equation}
\left\{
\begin{aligned}
& -t \Delta x<x_{1}-x_{L} & t \Delta x<x_{R}-x_{1} \\
& -t \Delta y<y_{1}-y_{B} & t \Delta y<y_{T}-y_{1}
\end{aligned}
\right.
\end{equation} $$

即
$$t d_{i}<q_{i} \quad i=1,2,3,4$$

$$\begin{array}{llll}
d_{1}=-\Delta x & d_{2}=\Delta x & d_{3}=-\Delta y & d_{4}=\Delta y \\
q_{1}=x_{1}-x_{L} & q_{2}=x_{R}-x_{1} & q_{3}=y_{1}-y_{B} & q_{4}=y_{T}-y_{1}
\end{array}$$

把被裁剪的红色直线段看成是一条有方向的线段，把窗口的四条边分成两类：
入边：左边界和下边界——从裁剪框外向裁剪框内
出边：右边界和上边界——从裁剪框内向裁剪框外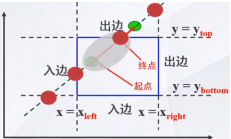
分情况讨论

$ d=0 :$
$ q<0 $, 说明直线与裁剪框平行，并且位于裁剪框的外面，直线为不可见，可抛弃，直接结束；
$ q\geq0 $，说明直线在它所平行的窗口边界的内部，还需进一步计算确定直线是否在窗口内、外、或者相交
$ d<0 $，说明直线是从裁剪边界的外部延伸到内部
$ d>0 $, 说明直线是从裁剪边界的内部延伸到外部
对于$ d\neq0 $，可以利用式子计算直线与边界k的交点的参数$ u $。对于每条直线，可以计算直线位于裁剪窗口内线段的参数$ d_1 $和$ d_2 $.
$ d_1 $的值是由那些使得直线是从外部延伸到内部的窗口边界决定。对于这些边计算$ r_i=q_i/d_i $，$ d_i= max(r_i,0) $.
$ d_2 $的值是由那些使得直线是从内部延伸到窗口边界决定，$ d_2=min(r_i,1) $.
如果$ d_1 $$ d_2 $这条直线完全在窗口的外面，不可见，可抛弃，否则，根据参数$ u $的两个值，计算出裁剪后线段的端点.

代码

代码的思路：画一个矩形，来作为一个裁剪窗口，然后画一条黄色的直线。如果直线没有经过矩形区域，则为黄色，如果穿过矩形区域，则使用Liang-Barskey算法来进行裁剪，裁剪之后，再进行画一条黑色的直线来覆盖。

/*liang-barsky.cpp*/
#include <iostream>
#include<GL/glut.h>
#include<Windows.h>
using namespace std;
#define ww 640   //屏幕的宽度
#define wh 480   //屏幕的高度
int xs, ys, xb, yb;
int rl = 200, rb = 200;
int rr = 400, rt = 400;
bool first;
//画线的方法
void lineNew(int x0, int y0, int xEnd, int yEnd)
{
  glClear(GL_COLOR_BUFFER_BIT);
  glColor3f(1.0f, 1.0f, 0.0f);  //画黄色
  glLineWidth(3);
  glBegin(GL_LINES);
  glVertex2f(x0, y0);
  glVertex2f(xEnd, yEnd);
  glEnd();

  glFlush();
}


void myDisplay() {

  glClear(GL_COLOR_BUFFER_BIT); //清空颜色缓冲池
  glColor3f(1.0f, 0.0f, 0.0f); //设置绘图颜色
  glRectf(rl,rb,rr,rt); //绘制矩形
  glFlush(); //执行OpenGL指令列表中的指令
}
bool ClipT(float p, float q, float *u1, float *u2) {
  float r;
  if (p < 0) {
    r = q / p;
    if (r > *u2) {
      return FALSE;
    }
    if (r > *u1) {
      *u1 = r;
    }
  }
  else if (p > 0) {
    r = q / p;
    if (r < *u1) {
      return FALSE;
    }
    if (r < *u2) {
      *u2 = r;
    }
  }
  else {
        return q >= 0;
  }
  return TRUE;
}

void LB_LineClip(float x1, float y1, float x2, float y2, float XL, float XR, float YB, float YT) {
  float dx, dy, u1, u2;
  u1 = 0;
  u2 = 1;
  dx = x2 - x1;
  dy = y2 - y1;
  if (ClipT(-dx,x1-XL,&u1,&u2)) {
    if (ClipT(dx, XR - x1, &u1, &u2)) {
      if (ClipT(-dy, y1 - YB, &u1, &u2)) {
        if (ClipT(dy, YT - y1, &u1, &u2)) {
          glLineWidth(3);
          glColor3f(0.0, 0.0, 0.0);//黑色
          glBegin(GL_LINES);

          glVertex2f(x1 + u1 * dx, y1 + u1 * dy);
          glVertex2f(x1 + u2 * dx, y1 + u2 * dy);
          glEnd();
          glFlush();
        }
      }
    }
  }
}
void Init() {
  glClearColor(1.0, 1.0, 1.0, 0.0); //即窗口的背景色
  glClear(GL_COLOR_BUFFER_BIT);      //清除颜色缓冲区，即窗口的背景色
  glMatrixMode(GL_MODELVIEW);
  glLoadIdentity();
  gluOrtho2D(0.0,ww, 0.0, wh);

}
void myMouse0(int button, int state, int x, int y)
{
  glBegin(GL_POINTS);
  if (button == GLUT_LEFT_BUTTON)
  {
    if (state == GLUT_DOWN) {
      xs = x;
      ys = wh - y;
      glVertex2i(xs, ys);
      first = 0;
    }
    else {
      xb = x;
      yb = wh - y;
      first = 1;
    }
    if (first) {
      lineNew(xs, ys, xb, yb);
      LB_LineClip(xs, ys, xb, yb, rl, rr, rb, rt);
    }

  }
  glEnd();
  glFlush(); //glFlush()清空缓冲区，将指令送往缓硬件立即执行
}

int main()
{
  glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
  glutInitWindowSize(ww, wh);
  glutInitWindowPosition(100, 150);
  glutCreateWindow("Liang-Barskey");
  Init();
  glutDisplayFunc(myDisplay);
  glutMouseFunc(myMouse0);

  glutMainLoop();  //持续显示，当窗口改变会重新绘制图形
  return 0;
}

Liang-Barsky裁剪算法

原理

代码

参考链接