扫描转换算法

DDA、中点画线、Bresenham算法

1 直线扫描转换算法

1.1 DDA算法

Digital Differential Analyer

在计算机光栅显示器上绘制一条直线$ y=kx+b $的本质是用一些离散的像素点去逼近这条直线，需要确定这些像素点的$ x $，$ y $坐标。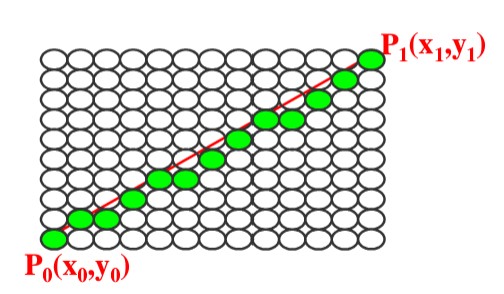

给出确定的两个端点$ \bigl(x_0,y_0\bigr) $和$ \bigl(x_1,y_1\bigr) $，即斜率$ k=\frac{y_1-y_0}{x_1-x_0} $
现假定$ x $已知，即从起点$ x_0 $开始，沿$ x $方向前进一个像素（步长=1），可以计算相应的$ y $值

注：因为像素的坐标是整数，而斜率$k$是浮点数，所以对于计算出的$ y $值需要进行取整处理

基本思想：

$ k\le1 $时，对$ x $值计算相应的$ y $值（对$ y $取整），从而确定需要给那些像素着色
$ k>1 $时，对$ y $值计算相应的$ x $值（对$ x $取整），从而确定需要给那些像素着色

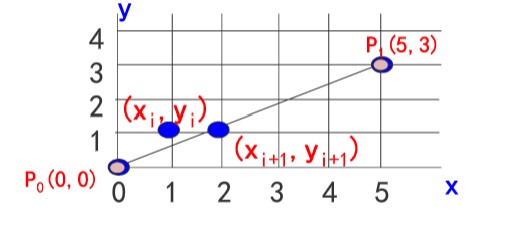
优化计算思想：增量思想

$ k\le1 $时,对于 $ y_i=kx_i+b $，$ y_{i+1}=kx_{i+1}+b=k(x_i+1)+b=y_i+k $，那么斜率$ k $即可看为前进一步的增量，这样就把将乘法运算变成了加法
$ k>1 $时，取$ x_{i+1}=x_i+\frac{1}{k} $即可

1.1.1 代码

#include<GL\glut.h>
#include<iostream>
#include<cmath>
using namespace std;

void init(void)
{
    glClearColor(1.0, 1.0, 1.0, 0.0);  // Set display-window color to white.
    glMatrixMode(GL_PROJECTION);       // Set projection parameters.
    gluOrtho2D(0.0, 200.0, 0.0, 150.0);
}

/*
    数值微分方法画线
*/
void LineDDA(int x1, int y1, int x2, int y2)
{
    glColor3f(1.0, 0.0, 0.0);       // 红色
    glPointSize(2.0f);

    /*
        两点重合尚未判断
    */
    int dm = 0;
    if (abs(x2 - x1) >= abs(y2 - y1))
    {
        dm = abs(x2 - x1);              // x 为计长方向
    }
    else
    {
        dm = abs(y2 - y1);              // y 为计长方向
    }
    float dx = (float)(x2 - x1) / dm;   // 当 x 为计长方向，dx = 1
    float dy = (float)(y2 - y1) / dm;   // 当 y 为计长方向，dy = 1
    float x = x1;
    float y = y1;

    for (int i = 0; i < dm; ++i)
    {
        glBegin(GL_POINTS);
        glVertex2f((int)x, (int)y);
        glEnd();
        glFlush();
        x += dx;
        y += dy;
    }
}

/*
    交换两个int 类型的变量的值
*/
void swap_value(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

// 窗口大小改变时调用的登记函数
void ChangeSize(GLsizei w, GLsizei h)
{

    if (h == 0)     h = 1;

    // 设置视区尺寸
    glViewport(0, 0, w, h);

    // 重置坐标系统
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();

    // 建立修剪空间的范围
    if (w <= h)
        glOrtho(0.0f, 250.0f, 0.0f, 250.0f*h / w, 1.0, -1.0);
    else
        glOrtho(0.0f, 250.0f*w / h, 0.0f, 250.0f, 1.0, -1.0);

}

/*

*/
void display(void)
{
    // 用当前背景色填充窗口，如果不写这句会残留之前的图像
    glClear(GL_COLOR_BUFFER_BIT);

    int x1 = 20, y1 = 20, x2 = 160, y2 = 80;
    LineDDA(x1, y1, x2, y2);
}

int main(int argc, char* argv[])
{
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
    glutInitWindowPosition(200, 200);
    glutInitWindowSize(400, 400);
    glutCreateWindow("Line");
    glutDisplayFunc(display);
    glutReshapeFunc(ChangeSize);
    init();
    glutMainLoop();
    return 0;
}

1.1.2 运行结果

1.2 中点画线算法

效率上最快

基本思想：采用直线的一般式方程$ F(x,y)=Ax+By+C=0 $
$ F(x,y)=Ax+By+C=0\le\left|k\right|\le1 $,$ x_i+1\rightarrow y_i \rightarrow \begin{cases}y_i \\y_i +1\end{cases}$，把浮点运算改成整数加法。

假定$ 0\le\left|k\right|\le1 $，沿$x$方向前进一个像素，$x_i \rightarrow x_i+1$，计算出$y_i \rightarrow \begin{cases}y_i \\y_i +1\end{cases} $.

当中点$M$在$Q$下方时，则$P_u$离直线近一些，选择$P_u$作为下一个像素点
当中点$M$在$Q$上方时，则$P_d$离直线近一些，选择$P_d$作为下一个像素点

判断$M$与$Q$的位置关系：将$M$点坐标代入方程有$d_i=A(x_i+1)+B(y_i+0.5)+C$

当$d_i\geq0$时选择$P_d$
当$d_i<0$时选择$P_u$

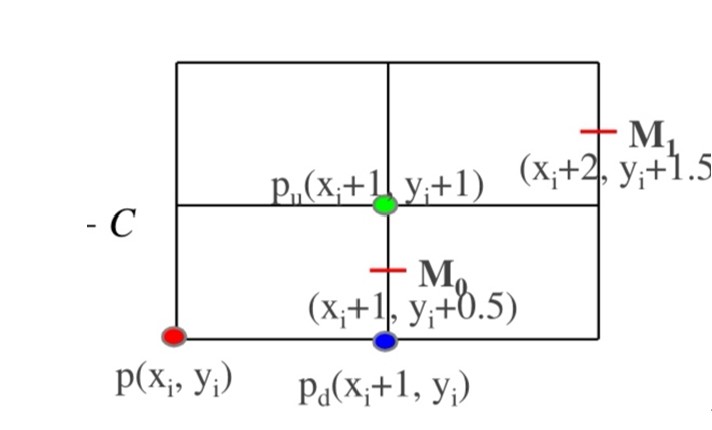
优化计算：$p(x_i,y_i)$在直线上即$Ax_i+By_i+C=0$，初值$d_0=F\left(x_i+1,y_i+0.5\right)=A+0.5B$

当选择了$P_u$作为像素点时，$d_0=F\left(x_i+1,y_i+0.5\right)$；$d_1=F\left(x_i+2,y_i+1.5\right)=d_0+A+B$
当选择了$P_d$作为像素点时，$d_0=F\left(x_i+1,y_i+0.5\right)$；$d_1=F\left(x_i+2,y_i+0.5\right)=d_0+A$

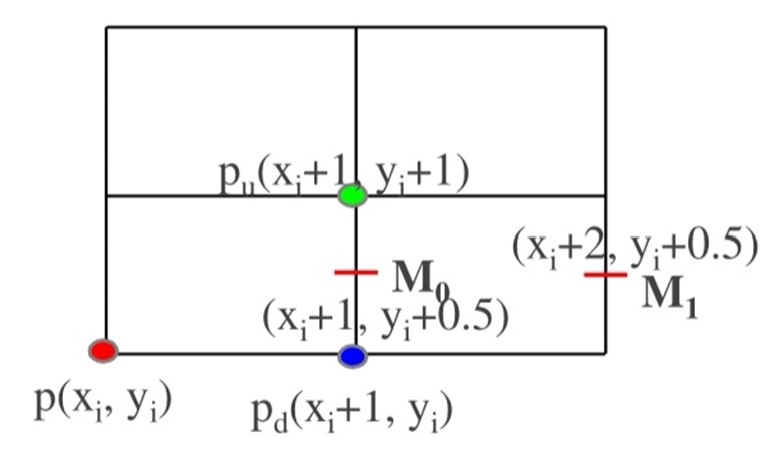
Bresenham算法

适用范围扩大，与方程无关不仅限于画直线

1.3 理论

DDA算法在编码实现比较容易，但是每生成一个像素都要用到一次浮点加法运算，Bresenham的线段光栅化算法可以避免浮点运算。

假设线段的起点$ \bigl(x_0,y_0\bigr) $和终点$ \bigl(x_1,y_1\bigr) $的坐标值都是整数，且斜率满足$ 0\leq m\leq 1 $
在线段扫描转换过程某一步中，假定已知$ (i+\frac{1}{2},j+\frac{1}{2}) $的像素。该线段所在的直线方程为$ y=mx+h $,当$ x=i+\frac{1}{2} $时，该直线与$ (i+\frac{1}{2},j+\frac{1}{2}) $处像素的垂直扫描线的实际交点是在垂直扫描线上位于该像素的半个像素内部的某一点（假定像素中心位置的坐标值位于两个整数之间），否则，对该实际交点进行四舍五入处理后不可能得到当前这个像素。

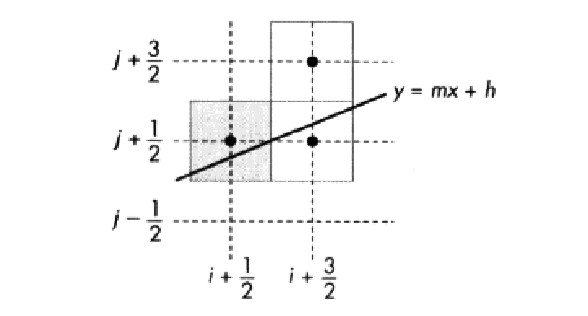
可以引入判定变量$ d=b-a $来判断下一个像素点的坐标，其中，$ a $和$ b $
表示在$x=i+\frac{3}{2}$号处，该线段分别离上方候选像素和下方候选像素的距离，如果$ d<0 $，那么线段靠近下方的像素，所以选择位于$ (x=i+\frac{3}{2},j+\frac{1}{2}) $处的下方像素；否则，应选择位于$ (i+\frac{3}{2},j+\frac{3}{2}) $处的上方像素.

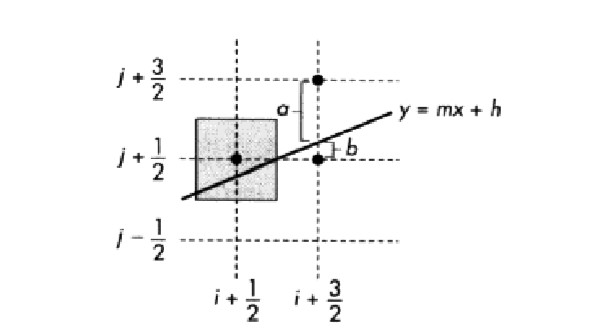
1.3.1 优化

定点运算代替浮点运算

令$ d=(x_2-x_1)(b-a)=\Delta x(b-a) $，用线段的方程将$ a $和$ b $的值代入，结合$ m=\frac{y_2-y_1}{x_2-x_1} $，$ h=y_2-mx_2 $，运算得$ d $为一整数（用到多次定点运算）

使该算法成为增量算法

假定$ d_k $是$ x＝k+\frac{1}{2} $号时对应的$ d $值。我们希望计算$ d_k $的增量形$ d_k+1 $，它是$ x=k+\frac{3}{2} $号时对应的$ d $值。

通过观察上方候选像素与直线之间的距离$ a $的值，当$ x=k+\frac{1}{2} $处像素的 $ y $坐标相对于前一个像素增加1，$ a $值增加$ 1-m $，或者减少$ m $。同理，当增加$ x $的值时，$ b $值要么增加$ m $，要么减少$ 1-m $。

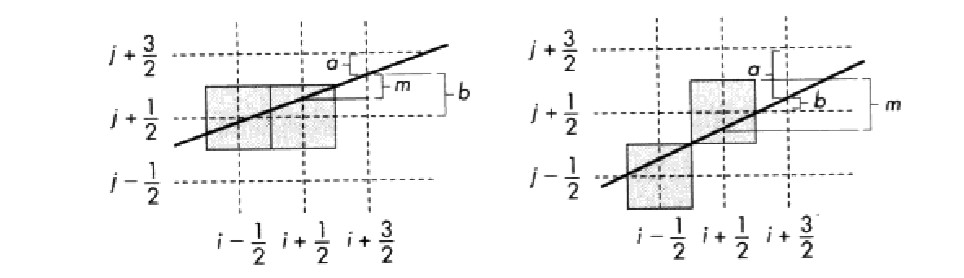
其中：
$$d_{k+1}=\begin{cases}
d_k+2\Delta y \qquad & d_k<0\\
2(\Delta y-\Delta x)\qquad & d_k\geq0
\end{cases} $$

1.3.2 代码

#include <windows.h>
#include <GL/glu.h>
#include <GL/gl.h>
#include <GL/glut.h>
#include<stdlib.h>

#include<GL\glut.h>
#include<iostream>
#include<cmath>
using namespace std;

void init(void)
{
    glClearColor(1.0, 1.0, 1.0, 0.0);  // Set display-window color to white.
    glMatrixMode(GL_PROJECTION);       // Set projection parameters.
    gluOrtho2D(0.0, 200.0, 0.0, 150.0);
}

/*
    交换两个int 类型的变量的值
*/
void swap_value(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

/*
    Bresenham 画线法
*/
void LineBres(int x1, int y1, int x2, int y2)
{
    glColor3f(0.0, 0.0, 1.0);       // 蓝色
    glPointSize(2.0f);

    int dx = abs(x2 - x1);
    int dy = abs(y2 - y1);
    // 两点重合
    if (dx == 0 && dy == 0)
    {
        glBegin(GL_POINTS);
            glVertex2f(x1, y1);
        glEnd();
        glFlush();
        return ;
    }

    int flag = 0;       // 将斜率变换到 0 <= |k| <= 1 区间
    if (dx < dy)
    {
        flag = 1;
        swap_value(&x1, &y1);
        swap_value(&x2, &y2);
        swap_value(&dx, &dy);
    }

    int tx = (x2 - x1) > 0 ? 1 : -1;
    int ty = (y2 - y1) > 0 ? 1 : -1;
    int curx = x1;
    int cury = y1;
    int dS = 2 * dy;
    int dT = 2 * (dy - dx);
    int d = dS - dx;
    while (curx != x2)
    {
        if (d < 0)
            d += dS;
        else
        {
            cury += ty;
            d += dT;
        }

        if (flag)
        {
            glBegin(GL_POINTS);
                glVertex2f(cury, curx);
            glEnd();
            glFlush();
        }
        else
        {
            glBegin(GL_POINTS);
                glVertex2f(curx, cury);
            glEnd();
            glFlush();
        }
        curx += tx;
    }

}

// 窗口大小改变时调用的登记函数
void ChangeSize(GLsizei w, GLsizei h)
{

    if (h == 0)     h = 1;

    // 设置视区尺寸
    glViewport(0, 0, w, h);

    // 重置坐标系统
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();

    // 建立修剪空间的范围
    if (w <= h)
        glOrtho(0.0f, 250.0f, 0.0f, 250.0f*h / w, 1.0, -1.0);
    else
        glOrtho(0.0f, 250.0f*w / h, 0.0f, 250.0f, 1.0, -1.0);

}

/*

*/
void display(void)
{
    // 用当前背景色填充窗口，如果不写这句会残留之前的图像
    glClear(GL_COLOR_BUFFER_BIT);
    int x12 = 20, y12 = 40, x22 = 160, y22 = 100;
    LineBres(x12, y12, x22, y22);
}

int main(int argc, char* argv[])
{
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
    glutInitWindowPosition(200, 200);
    glutInitWindowSize(400, 400);
    glutCreateWindow("Line");
    glutDisplayFunc(display);
    glutReshapeFunc(ChangeSize);
    init();
    glutMainLoop();
    return 0;
}

1.3.3 运行结果

2 多边形扫描转化算法

多边形分为凸多边形，凹多边形（任意两顶点间的连线有不在多边形内的部分）含内环的多边形

2.1 X扫描线算法

多边形扫描转换指的是把多边形的顶点表示转换为点阵表示

基本思想：按扫描线的顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的像素，完成填充工作。端点即为扫描线与多边形边界线的交点。
算法步骤：

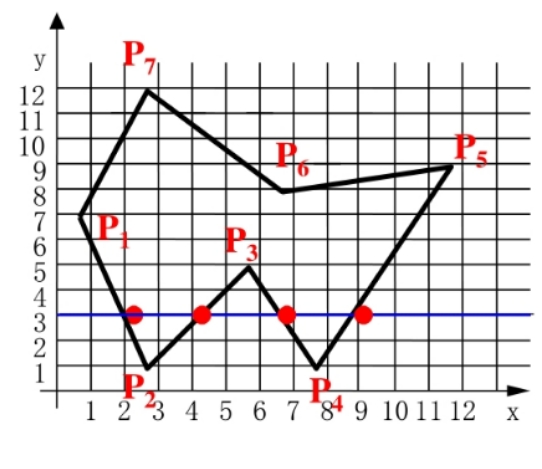
（1）确定多边形所占有的最大扫描数，得到多边形顶点的最小和最大值
（2）从 $y=y_{min}$ 到 $y=y_{max}$ 每次用一条扫描线进行填充
（3）扫描线的填充过程：求交排序（交点按递增顺序排）$\to$交点配对（偶数个）$\to$区间填色

当扫描线与某一顶点相交时，交点的取舍问题处理办法为：
共享顶点的两条边分别落在扫描线左右两边，交点只算1个
共享顶点的两条边的另外两个端点值大于顶点值，交点算2个，否则算0个
缺点：扫描线与多边形各边求交很麻烦

2.2 改进的X扫描线算法（不求交）

改进求交方法：
（1）只与有效边求交；
（2）扫描线的连贯性——当前扫描线与各边交点顺序与下条扫描线与各边交点顺序雷同;
（3）多边形的连贯性——某条边与当前扫描线相交时很可能也与下一条扫描线相交.
引进数据结构：
（1）活性边表——与当前扫描线相交的边叫做活性边，并把他们按与扫描线交点，坐标递增的顺序存放在一个链表中
（2）结点内容——$x$（交点坐标）；$\delta{x}$（相邻扫描线的增量）；$y_{max}$（最高扫描线的坐标值）

$$ x \to \delta x \to y_{max} \to \text { Next } $$

扫描线一次向上移动1，即$y_{i+1}-y_{i}=1$ ，相交直线边斜率为$k$，即$x_{i+1}=x_{i}+\frac{1}{k}$
其中$\delta=\frac{1}{k}$ ，而$y_{max}$可以确定何时抛弃该有效边

构建新边表：构造纵向链表，链表长度为多边形所占有的最大扫描线数
对扫描线出现的位置构造

$$ y_{max} \to x_{min} \to \frac{1}{k} \to \text { Next } $$

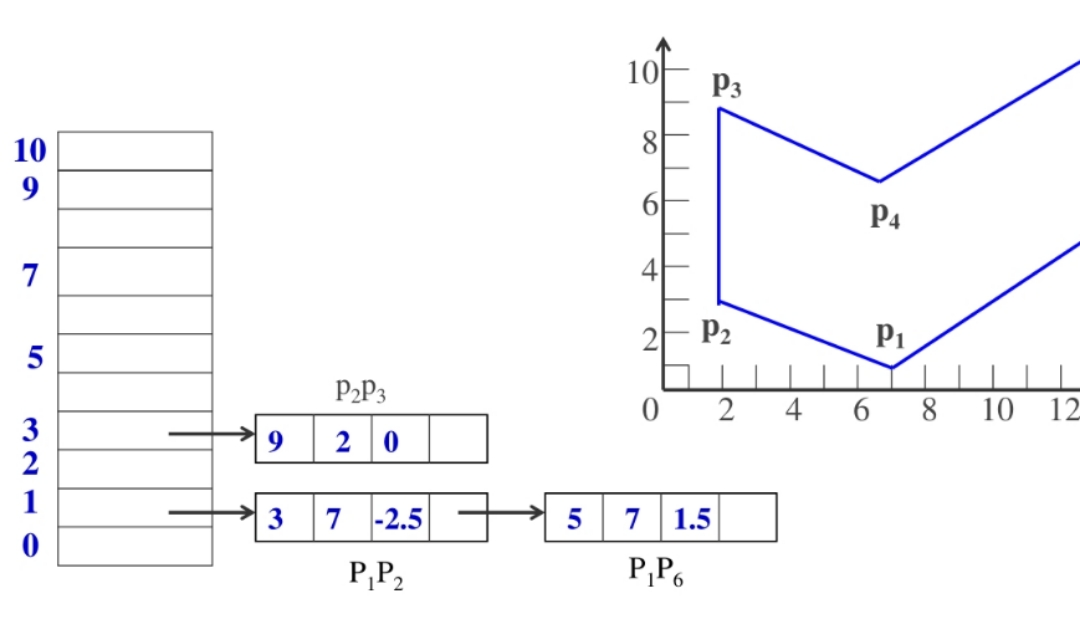
注：边是否被抛弃，未抛弃则要注意，还要看是否有新边进来

2.3 区域填充算法

要求区域内连通

区域可分4连通（左上右下）和8连通（斜方向）区域

简单四连通种子填充算法（区域填充递归算法）：
使用栈结构来实现：栈顶像素出栈$\to$将出栈像素置成要填充色$\to$按左上右下顺序将不在边界且未填充的像素入栈填充$\to$对最后一个入栈的像素重复上述操作
多边形扫描转换算法与区域填充算法的区别
区域填充需要一个种子点，根据区域连通性进行颜色扩散
扫描线转换是从边界出发采用多种形式的连贯性进行填充

参考链接

中国大学MOOC