Cohen-Sutherland编码裁剪

Posted on | In | 1k | 5 分钟

一类编码裁剪算法

1 二维剪裁

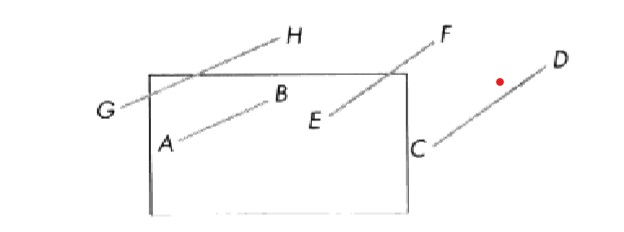
二维剪裁是在三维线段投影到投影平面之后才进行的，并且剪裁窗口是投影平面的一部分，该投影片面投影到屏幕的视口中，所有的值都可用实数表示。AB整段显示，CD整段不显示，EF和GH裁剪后显示

2 原理

为避免求交（所在直线与剪裁窗口各条边的交点）运算，Cohen-Sutherland算法使用浮点减法与位操作相结合的方式代替大量浮点乘法和除法的裁剪算法。
该算法把裁剪窗口的四条边延长，将二维空间分割成9个区域，并赋予每个区域一个唯一的四位二进制数（编码），编码的4位分别代表端点位于窗口的上、下、右、左。

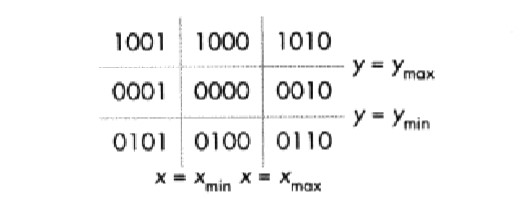
考虑线段$ o_1 $$ o_2 $,对两端点的编码情况进行讨论，有四种情况：

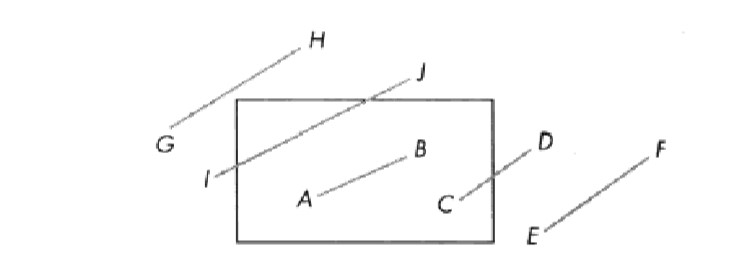
  1. 若点$ o_1 $和$ o_2 $完全在裁剪窗口内，则保留该直线，如线段AB，然后进行光栅化处理
  2. 若点$ o_1 $和$ o_2 $有一个端点在裁剪窗口内，如线段CD，非零的端点编码说明线段与剪裁窗口的哪条边或拿两条边相交判断是否要进行两次求交运算
  3. 若$ o_1 $和$ o_2 $均不为0，对两个端点编码按位与运算，判断是否在同一侧，若是舍弃，如线段EF
  4. 如果直线段既不满足保留的条件，也不满足舍弃的条件？那么需要对直线段按交点进行分段，分段后判断直线是保留还是舍弃。（如GH与IJ)

当要处理的线段很多，而实际显示的线段很少时，Cohen-Sutherland算法非常有效

3 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
#include<gl/glut.h>
#include<stdio.h>
#include<stdlib.h>

#define LEFT_EDGE 1
#define RIGHT_EDGE 2
#define BOTTOM_EDGE 4
#define TOP_EDGE 8

void LineGL(int x0, int y0, int x1, int y1){
  glBegin(GL_LINES);
  glColor3f(1.0f, 0.0f, 0.0f); glVertex2f(x0, y0);
  glColor3f(0.0f, 1.0f, 0.0f); glVertex2f(x1, y1);
  glEnd();
}

struct Rectangle{
  float xmin, xmax, ymin, ymax;
};

Rectangle rect;
int x0, y0, x1, y1;

int CompCode(int x, int y, Rectangle rect){
  int code = 0x00;
  if (y < rect.ymin)
    code = code | 4;
  if (y>rect.ymax)
    code = code | 8;
  if (x>rect.xmax)
    code = code | 2;
  if (x<rect.xmin)
    code = code | 1;
  return code;
}
int cohensutherlandlineclip(Rectangle rect, int &x0, int &y0, int &x1, int &y1)
{
  int accept, done;
  float x, y;
  accept = 0;
  done = 0;

  int code0, code1, codeout;
  code0 = CompCode(x0, y0, rect);
  code1 = CompCode(x1, y1, rect);
  do{
    if (!(code0 | code1)){//整条线段在窗口内
      accept = 1;//取之
      done = 1;
    }
    else if (code0 & code1)//两个端点同在窗口一侧，弃之
      done = 1;
    else{//线段与窗口存在交点
      if (code0 != 0)
        codeout = code0;
      else
        codeout = code1;
            //求交点
      if (codeout&LEFT_EDGE){
        y = y0 + (y1 - y0)*(rect.xmin - x0) / (x1 - x0);
        x = (float)rect.xmin;
      }
      else if (codeout&RIGHT_EDGE){
        y = y0 + (y1 - y0)*(rect.xmax - x0) / (x1 - x0);
        x = (float)rect.xmax;
      }
      else if (codeout&BOTTOM_EDGE){
        x = x0 + (x1 - x0)*(rect.ymin - y0) / (y1 - y0);
        y = (float)rect.ymin;
      }
      else if (codeout&TOP_EDGE){
        x = x0 + (x1 - x0)*(rect.ymax - y0) / (y1 - y0);
        y = (float)rect.ymax;
      }
      //舍弃在窗口外的部分线段
      if (codeout == code0){
        x0 = x; y0 = y;
        code0 = CompCode(x0, y0, rect);
      }
      else
      {
        x1 = x; y1 = y;
        code1 = CompCode(x1, y1, rect);
      }
    }
  } while (!done);
    if (accept)
    LineGL(x0, y0, x1, y1);
  else{
    x0 = 0; y = 0; x1 = 0; y1 = 0;
    LineGL(x0, y0, x1, y1);
  }
  return accept;
}

void myDisplay(){
  glClear(GL_COLOR_BUFFER_BIT);
  glColor3f(1.0f, 0.0f, 0.0f);
  glRectf(rect.xmin, rect.ymin, rect.xmax, rect.ymax);

  LineGL(x0, y0, x1, y1);

  glFlush();
}
void Init(){
  glClearColor(0.0, 0.0, 0.0, 0.0);
  glShadeModel(GL_FLAT);

  rect.xmin = 100;
  rect.xmax = 300;
  rect.ymin = 100;
  rect.ymax = 300;

  x0 = 450, y0 = 0, x1 = 0, y1 = 450;
  printf("Press key 'c' to Clip!\nPress key 'r' to Restore!\n");

}

void Reshape(int w, int h){
  glViewport(0, 0, (GLsizei) w, (GLsizei) h);
  glMatrixMode(GL_PROJECTION);
  glLoadIdentity();
  gluOrtho2D(0.0, (GLdouble)w, 0.0, (GLdouble)h);
}

void keyboard(unsigned char key, int x, int y){
  switch (key){
  case 'c':
    cohensutherlandlineclip(rect, x0, y0, x1, y1);
    glutPostRedisplay();
    break;
  case 'r':
    Init();
    glutPostRedisplay();
    break;
  case 'x':
    exit(0);
    break;
  default:
    break;
  }
}

int main(int argc, char *argv[]){
  glutInit(&argc, argv);
  glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
  glutInitWindowPosition(100, 100);
  glutInitWindowSize(640,480);
  glutCreateWindow("Cohen-Sutherland");

  Init();
  glutDisplayFunc(myDisplay);
  glutReshapeFunc(Reshape);
  glutKeyboardFunc(keyboard);
  glutMainLoop();
  return 0;
}

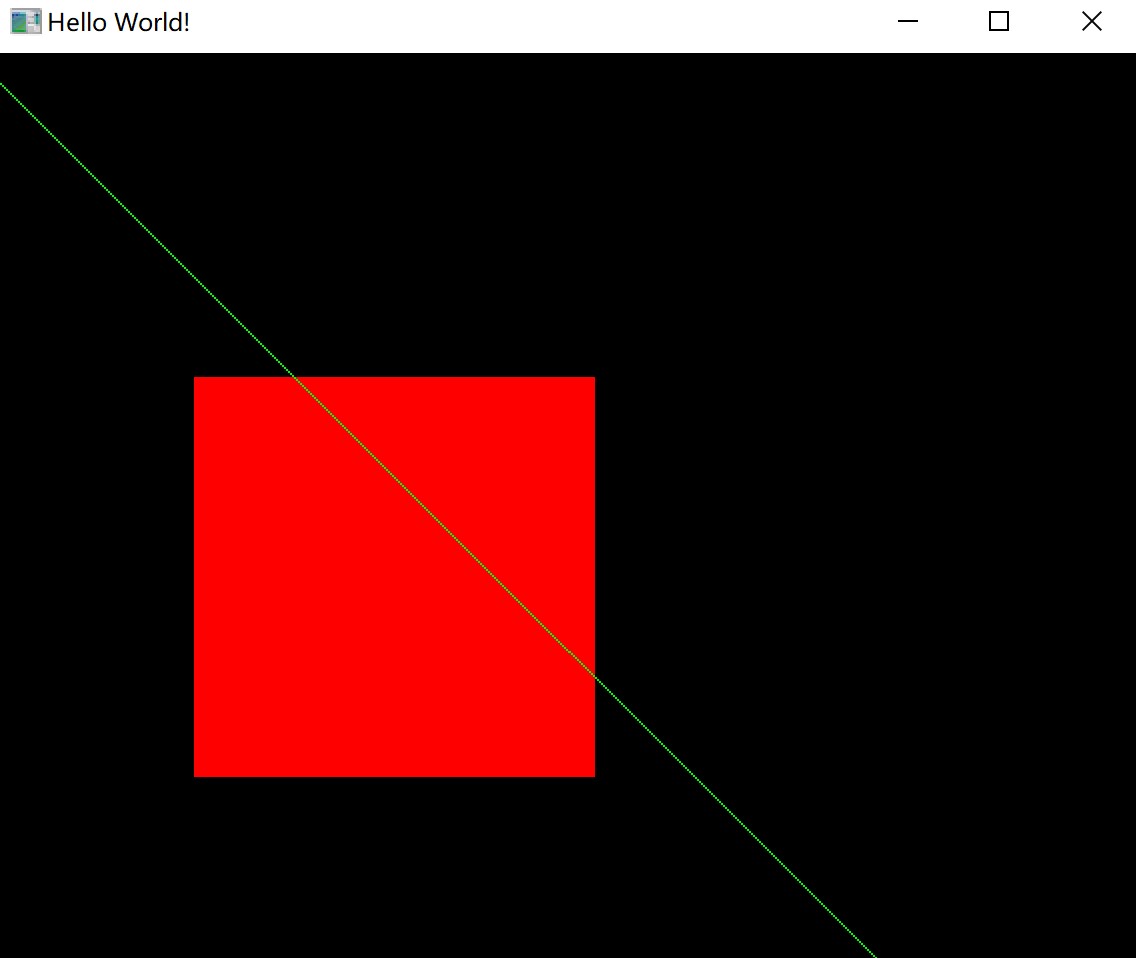
4 运行结果

参考链接

  1. 计算机图形学-直线裁剪Cohen-Sutherland编码裁剪算法
-------------------本文结束 感谢您的阅读-------------------
0%